In the summer of 2024, I was selected to participate in Penn State's physics REU. I developed a simulation of a quantum circuit from scratch with Dr. Sarah Shandera. When evolving the state of a whole system of qubits, you often apply unitary operations between groupings of them. From this, you can derive what are called dynamical maps, which equivalently evolve the state of single qubits in the circuit. From the whole system of qubits, you can determine how individual qubits evolve. When tracking the evolution of a single qubit, however, you must effectively average over the effects of its environmental qubits, so if there is a great degree of entanglement between your qubit of interest and its environment, this action of averaging over the state over the environment will inherently lose some information about the state of your system. Because some of your system's information can be lost in this process of deriving single qubit maps, these maps need not be unitary. This additionally gives rise to a mathematical property called non-complete positivity on the single qubit maps. If a map is not completely positive, it is not true that you will always have a valid quantum state after evolving an initially valid state over the single qubit map for all possible initial states. Because of this, the arrival of this mathematical property is thought to be indicative of the dynamics of higher-order entanglement (entanglement between more than two qubits), which we don't fully understand. My job was to first write code that simulated an n-qubit circuit, derive the condition for our single qubit maps to be non-completely positive, and try to determine if the arrival of these non-completely positive maps had anything to do with possible diagnoses for higher-order entanglement.
To attempt connecting the arrival of NCP maps to potential signs of higher order entnaglement, I began by writing a quantum circuit simulation from scratch in Python. To do this, I made use of the qutip toolkit, setting up all of my variables and operators in it, which allowed me to easily carry out the more niche operations to quantum information and computation, such as the partial trace and the tensor product. Evolving my circuit in a brickwork pattern of unitaries, which is standard in the field, I first tensored up two separate large operators which would replicate the effect of the even and odd time steps in the circuit (which have different unitary patterns). I wrote my states in the thermal matrices that my mentor was interested in studying, went on to deriving the property that would correspond to the arrival of NCP maps (which took a couple of weeks to correct), and wrote up code to animate my circuit, which tracked whether or not a map was NCP using lights in the circuit; green to indicate a map was CP and red to indicate a map was NCP.
Animating the evolution of a circuit and deriving the dynamical maps between the initial and final state of each qubit at each time in the simulation. When a dynamical map is NCP, it is marked red. Note how rare such an occurrence is for our system of interest.
As I began to feel that the work was close to complete, I didn't have the opportunity to see my mentor very often, so I began defining all kinds of thermodynamic and information-theoretic properties on the circuit so that I could track the arrival of NCP maps, which I had derived the condition for, with some characteristic pattern in some of these defined properties. My thought was that the arrival of NCP maps would be indicative of a property like mutual information spiking between pairs of qubits, thus indicating where the multipartite entanglement generating the NCP map was coming from. I had quickly developed a simulation that produced a massive amount of data, so I began doing what I know best and performed all kinds of data analysis techniques to search for the connection between NCP maps and anything happening to these properties.
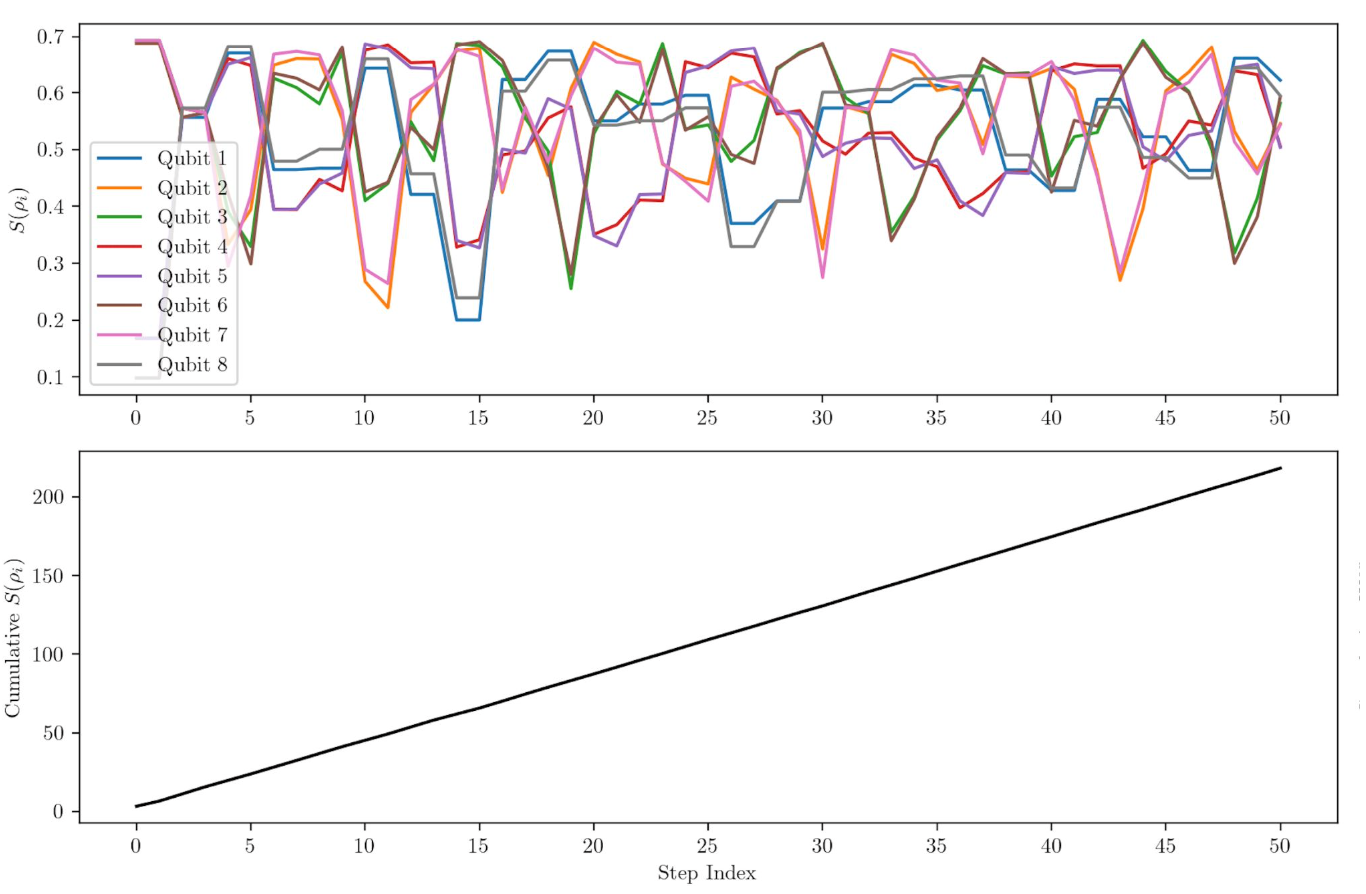
Showing the entropy of individual qubits fluctuating over time and showing that the cumulative entropy of the whole circuit grows linearly over time, matching a proven result for quantum circuits.
Animation of the mutual information shared between qubit pairs changing as circuit evolves. Nodes represent individual qubits, edges represent whether or not they share mutual information (whether or not they are entangled), and the distance between nodes represents the mutual information's magnitude.
I ended the experience by creating a method by which I could compute a correlation between the arrival of NCP maps and a spike in the mutual information between specific qubits pairs. My thought was that when an NCP map would arrive, if it was a signal for higher-order entanglement, there may be a spike in mutual information between the qubits that this higher order entanglement was present between. In carrying this out, I discovered that such a correlation did not exist, and similarly did not exist for another measure of mutlipartite entanglement called concurrence.
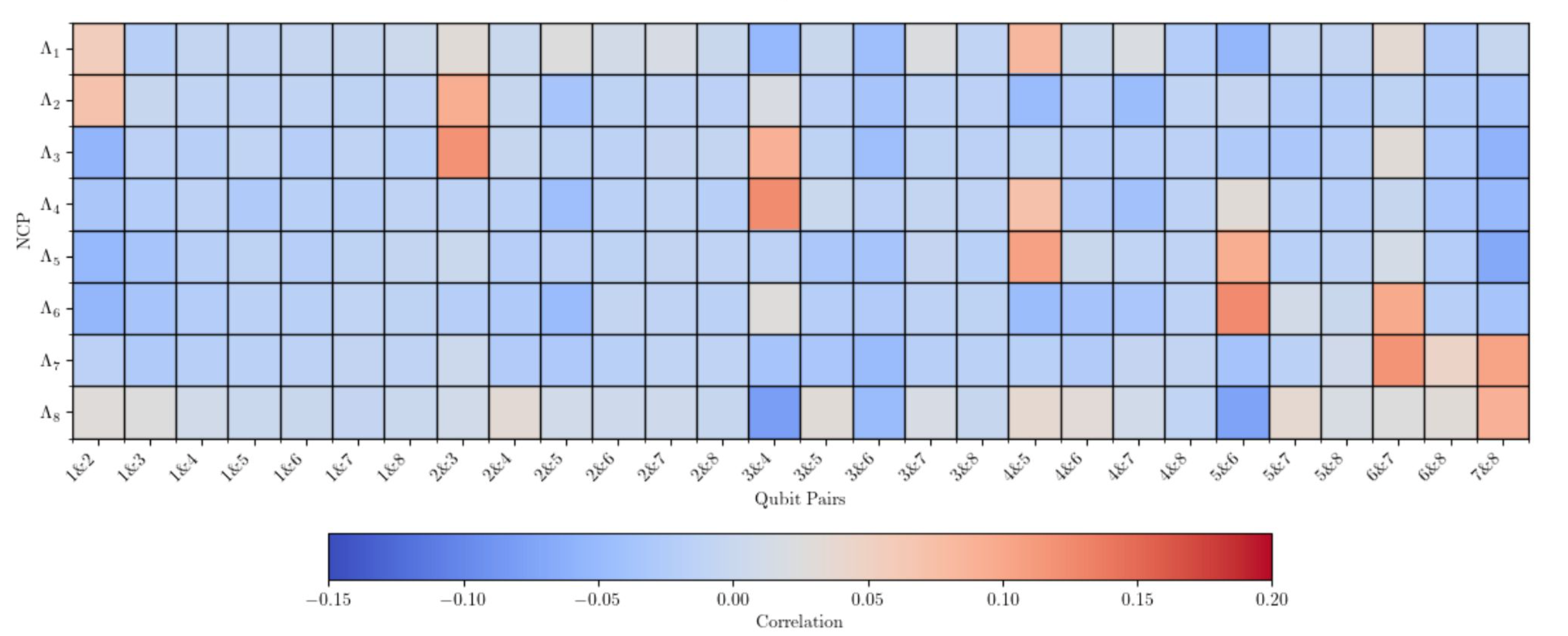
Showing the lack of correlation between mutual information (measure of bipartite entanglement) spikes and the arrival of NCP maps. Generated with incorrect derivation of NCP maps which was generating NCP maps at a much higher frequency and still features a poor correlation.
Approaching this project without any prior experience in quantum research proved to be an enjoyable and occasionally frustrating challenge. The ability to come up to speed with a foreign field of research in a relatively short period of time either comes from innate genius or is a skill learned over many attempts, so it's this skill that I am the most grateful for having had the chance to develop. Starting the summer with an empty Jupyter cell was another enjoyable challenge that has given me some pride in the simulation and tools that were developed during the project.