General relativity has been one of the most successful theories in the history of physics, having passed countless observational tests. Despite its success, however, there still exist fundamental problems with the theory in the form of singularities that have been proven to exist at the center of black holes and at the origin of our universe. General relativity additionally faces problems in the discrepancy between astronomical observations and predictions for these events generated by the theory. These have ultimately led to the hypothesized existence of dark matter and dark energy. Despite the mounting evidence for dark matter's existence, some physicists believe that hypothesizing the existence of dark matter from the current observational challenges is an overstepping of theoretical expectations, and instead propose that these challenges could be solved by adding modifications to general relativity.
For my senior thesis in mathematics, I knew I wanted to work on a problem in gravitational theory, but without given a canned project in the field, I spent some of the last few weeks before the fall semester began figuring out what work I found interesting and that I would be able to reasonably accomplish within around a semester given my working knowledge of general relativity. Having some interest in computational physics, I decided to read up on the math used to create simulations of gravitational systems, called numerical relativity. I learned that in order to simulate Einstein's equations on a computer, one needs to write his field equations in a formalism conducive to describing a system's spatial and temporal evolution separately. In this way, one needs a method for separating the spatial and temporal components of the theory's variables, which is achieved by applying what is called the 3+1 decomposition to the theory. This 3+1 decomposition is a generic method and so I decided on finding a modified theory that had not yet had this method applied to it. When this decomposition is fully applied to a theory of gravity, it is then written in an ADM formulation, which is named after the authors who first worked this out for general relativity.
I spent the first couple of weeks into the fall semester looking for a modified theory of gravity that I could reasonably work with, and eventually landed on John Moffat's Scalar-Tensor-Vector Gravity (STVG).
When one applies the 3+1 decomposition to a theory of gravity, three separate decompositions are required to be made for each of the theory's variables after some notion of the direction in which time flows is established. One needs to project all of the theory's variables (1) all along the spatial components, (2) all along the direction of the normal vector which defines the direction of time flow, and (3) one needs to compute a mixed project: one that projects your theory's variables along the spatial and normal directions.
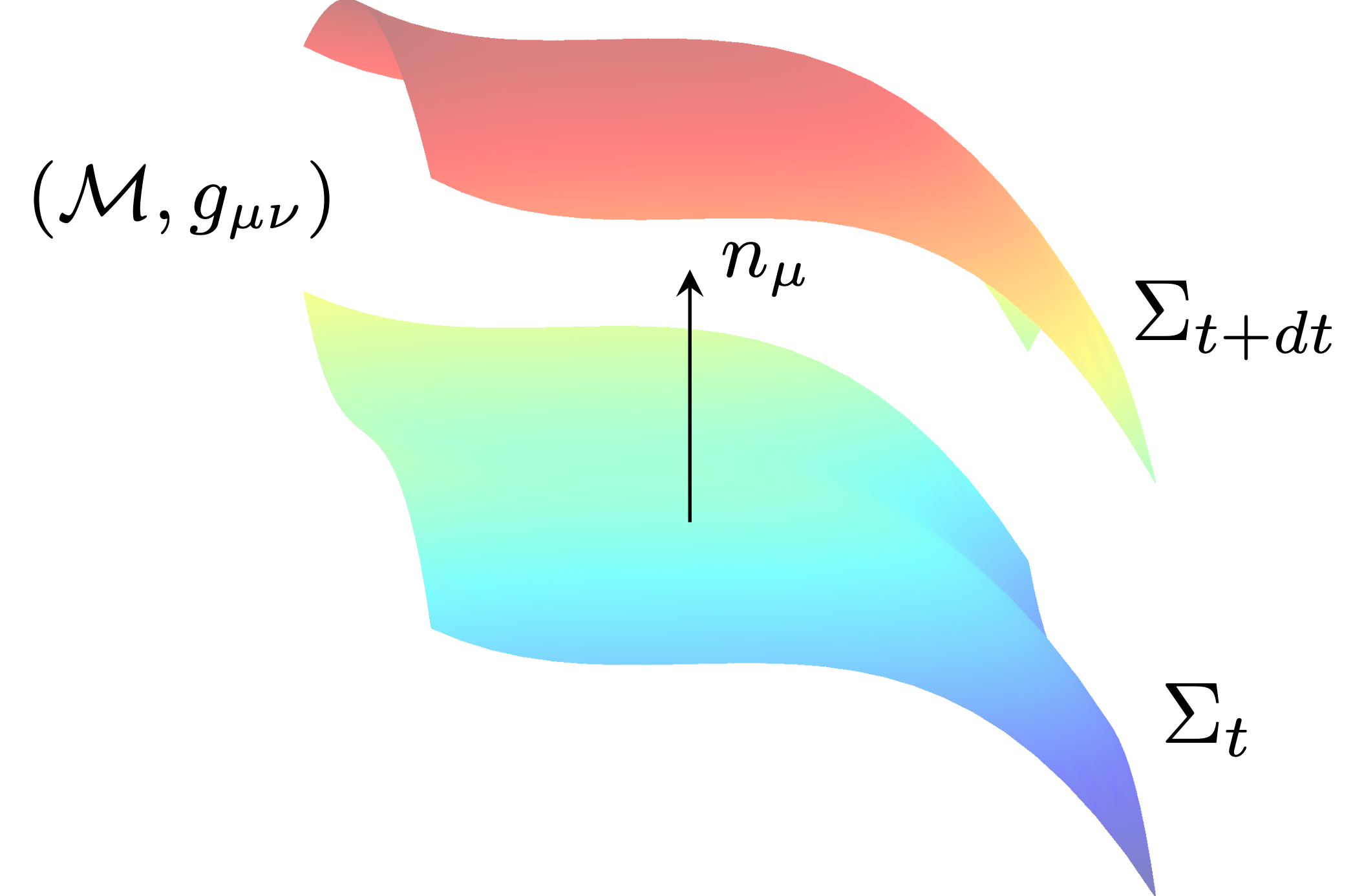
Foliating a manifold into spatial hypersurfaces that evolve over time to apply the 3+1 decomposition
SVTG adds three scalar terms, one of which allows the gravitational constant G to vary over space and time, and one vector field, which adds a repulsive gravitational force to the theory, in addition to modifying the original tensor field equations handed down to us from Einstein. Because of this, to fully decompose SVTG, and therefore write it in the ADM formulation, there are five field equations that need to be decomposed and there are three decompositions that are needed to be made for each, meaning my thesis work consists of fifteen total computations that need to be carried out.
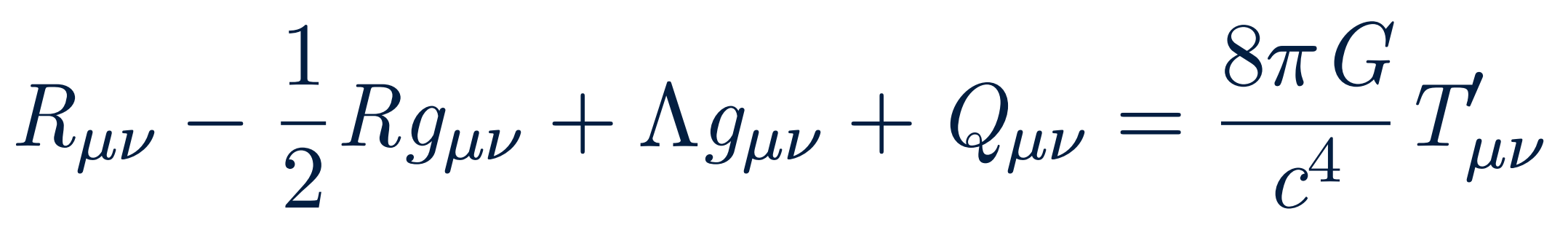
The tensor field equations for Scalar-Tensor-Vector Gravity
Working on a math thesis on a rigorous subject without the guidance of an advisor in the field has challenged me in a constructive way, especially being in a field that I would like to stay close to in grad school. I don't intend in any way to continue this work in grad school, but having more advanced knowledge of differential geometry and mathematical relativity will support my future goal of working on some aspect of theoretical relativity or cosmology. Given that most relativity theorists work closely with simulation, having a working knowledge of numerical relativity and its mathematical basis, the 3+1 formalism, will also support my future goals in this way. I see this work as a culmination of a good amount of physics, and especially math, I have learned while at Carthage. Working on this thesis has required a knowledge of the 3+1 formalism, which requires a good knowledge of general relativity, which itself requires a strong background in multivariable calculus and the more advanced methods introduced later in the Electricity and Magnetism class at Carthage.